“Vispārīgā
bioloģija”, “Dzīvības
ķīmija, šūna”
2. laboratorijas darbs.
Aprēķinu piemēri.
2. tabula.
Paraugu masas izmaiņas pēc žāvēšanas un noteiktais
ūdens/ sausnas saturs paraugos.
| Nr. |
paraugs |
sverglāzes |
Parauga iesvara masa (g) | glāze + sausais paraugs (g) |
sausnas masa (g) |
sausna svaigā paraugā (%) | ūdens svaigā paraugā (%) |
| P |
XXX |
20,00 |
0,50 |
20,15 |
0,15 |
30,0 |
70,0 |
Produktu sausnas un ūdens satura
aprēķini.
Aprēķinu
piemērs dots atbilstoši kāda nezināma parauga “XXX” (Nr.
P) sausnas un ūdens satura aprēķinu gaitai.
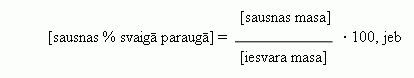
[sausnas %
svaigā paraugā] = (0,15/0,50) · 100 = 30
(%)
3.
Aprēķinam ūdens saturu (%) svaigajā paraugā:
Tā kā visa
svaigā parauga masa tiek pieņemta par 100%, tad
[ūdens % svaigā paraugā] = 100 - [sausnas %
svaigā paraugā], jeb
[ūdens % svaigā paraugā] = 100 - 30 = 70 (%)
3. tabula.
Dati optiskā blīvuma un proteīnu masu saistošā grafika
konstruēšanai.
|
BSA koncentrācija (mg/ml) |
proteīni 20 µl šķīduma (µg) |
|
|
|
|
|
0,05 |
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
0,7 |
|
|
|
|
|
Koncentrācijas / masas aprēķini.
Lai
veidotu grafiku, kas parāda nomērītā optiskā blīvuma
saikni ar proteīnu daudzumu, mums jāzin, cik daudz
proteīnu tika ievadīts Bradfordas reakcijā.
Bradfordas
reakcijai visos gadījumos tika ņemti 20 ml testējamā
šķīduma. Tātad jāaprēķina cik mg proteīnu
atrodas 20 ml šķīduma,
ja tā koncentrācija ir, piemēram, 0,7 mg/ml.
Dotā koncentrācija norāda, ka katrā šī šķīduma
mililitrā atrodas 0,7 mg BSA (proteīnu).
Ērtības
labad varam:
1 ml
izteikt µl.
1 ml = 1 000 µl,
savukārt
0,7 mg izteikt µg
0,7 * 1 000 = 700 µg.
Tālāk varam
sastādīt proporciju:
1000 µl šķīduma ar
koncentrāciju 0,7 mg/ml atrodas 700 µg proteīnu.
20 µl šķīduma
ar koncentrāciju 0,7 mg/ml atrodas X µg proteīnu.
Risinot
proporcijas, nezināmo X atrod pilnās diagonāles vērtības
(700 µg un 20 µl)
sareizinot un reizinājumu izdalot ar nepilnās (tās, kurā
ir nezināmais) diagonāles zināmo vērtību (1000 µl):
X = (700 · 20) / 1000
= 14 (µg)
| Nr. |
iesvara masa
proteīnu ekstraktam |
|
proteīni 20 µl šķīduma (µg) |
|
|
|
proteīni % no sausnas masas (%) |
| P |
0,250 |
5,0 |
4,0 |
0,2 |
1,0 |
0,4 |
1,3 |
Proteīnu daudzuma aprēķini paraugos.
Aprēķināmie
lielumi 4 . tabulā izcelti ar uzbiezinātu tekstu.
1. Aprēķinam
proteīnu koncentrāciju mērītajā paraugā (mg/ml).
Izmantojot 4. tabulas stabiņa “proteīni 20 µl šķīduma (µg)” skaitlisko vērtību "4,0", kura nolasīta no
grafika, varam sastādīt proporciju:
20 µl
proteīnu šķīduma atrodas
4 µg
proteīnu.
1000 µl
proteīnu šķīduma atrodas
X µg proteīnu.
Risinot
proporcijas, nezināmo X atrod pilnās diagonāles vērtības
(1000 µl un 4 µg)
sareizinot un reizinājumu izdalot ar nepilnās (tās, kurā
ir nezināmais) diagonāles zināmo vērtību (20 µl):
X = (1000 · 4) / 20 =
200 (µg)
Tātad 1 ml
(1000 µl) šķīduma
atrodas 200 µg proteīnu.
Šo
koncentrāciju pārveidojot prasītajās mērvienībās
iegūstam 200
µg/ml = 0,2 mg/ml
2.
Aprēķinam
proteīnu koncentrāciju
(mg/ml) šķīdumā pirms atšķaidīšanas.
Tie produktu
šķīdumi (lizāti), kuros bija sagaidāma liela proteīnu
koncentrācija, pirms Jūs tos saņēmāt
mērīšanai, tika atšķaidīti. Atšķaidījuma reižu skaits
dots 4. tabulas stabiņā “ atšķaidījums reizes (x)".
Ja
sākotnējais lizāts mērīšanai ticis atšķaidīts 5 reizes,
tad iegūto
koncentrāciju pareizina ar atšķaidījuma reižu skaitu:
[proteīnu
koncentrācija pirms
atšķaidīšanas] = [koncentrāciju
mērītajā
paraugā] ·
[atšķaidījums reizes]
[proteīnu
koncentrācija pirms
atšķaidīšanas] = 0,2 ·
5
= 1,0
(mg/ml).
3.
Aprēķinam
proteīnu
daudzumu 100 g svaiga produkta (g/100g).
Zinot, ka produktu
lizāti iegūti produkta iesvaram pievienojot 1N NaOH
šķīdumu tā, lai kopējais tilpums būtu 1 ml, un to, ka
parauga iesvars lizātā bija vienīgais proteīnu avots,
varam secināt, ka lizāta vienā mililitrā noteiktais
proteīnu daudzums atradies svaigā parauga iesvarā, kura
masa dota 4. tabulā.
Tātad, dotajā piemērā 1
mg proteīnu atrodas 0,25 g svaigā produkta (4. tabula,
stabiņš “iesvara masa proteīnu ekstraktam (g)”).
Varam
sastādīt proporciju:
0,25 g svaigā produkta satur 1,0 mg proteīnu
100,00 g svaigā produkta satur X mg proteīnu
X = (100,00·1) / 0,25 =
400 (mg)
Tā kā
proteīnu masa tiek prasīta gramos, veicam pārveidojumu:
4.
Aprēķinam
proteīnu
daudzumu % no produkta sausnas masas.
Iepriekš
tika noteikts, ka produkts P satur 30% sausnas (1.
tabula).
Izmantojot
šo rezultātu varam izteikt, cik gramus sausnas satur 100
g svaigā produkta:
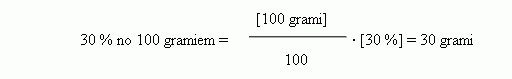
Tātad, 100
grami attiecīgā produkta satur 30 gramus sausnas.
4.
tabulas stabiņā “proteīnu daudzumu
100 g svaiga produkta (g/100g)” jau ierakstījām, ka 100
g svaiga produkta satur 0,4 gramus proteīnu.
No šiem
abiem lielumiem varam izrēķināt, cik % no šī produkta
sausnas masas veido proteīni.
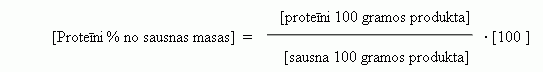
[Proteīni % no
sausnas masas] = (0,4/30) · 100 = 1,3 %
|
LU Bioloģijas fakultāte
Mikrobioloģijas un biotehnoloģijas katedra
M. Lazdiņš |