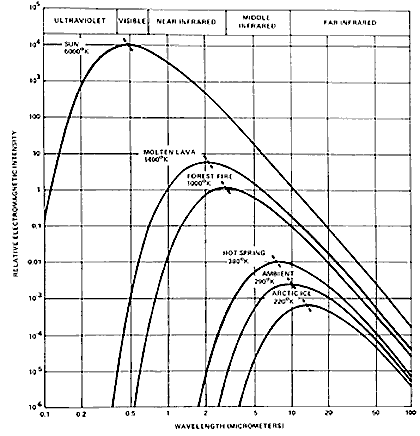
The above figure (shown earlier on page 8-8) plots spectral wavelength vs. emitted radiance (as intensity) from thermal radiators at various peak radiant temperatures ranging from that of the Sun through the Earth's surface (average ambient temperature) to sea ice . The hotter the radiating body, the greater is the radiance (intensity on the ordinate) over its range of wavelengths and the wavelength at which peak emission occurs moves to shorter wavelengths. The relation between peak wavelength and radiant body temperature is known as the Wien Displacement Law:

where is the wavelength at maximum radiant emittance and T is the absolute temperature in degrees Kelvin ( °C + 273). (The constant, 2898 is in units of µm °K; it is also given as [rounded off] 0.29 cm °K.) For the Sun, with a photospheric radiant temperature of ~6000 °K, this peak is in the visible (ca 0.58 µm); a forest fire peaks around 5.0 µm; the Earth as observed from space peaks within the 8-14 µm interval.

The radiant flux F_r emanating from a body is related its internal (kinetic) temperature T_k by the Stefan-Boltzmann Law, which in simplified form is given as F_r = sT_k⁴, where s (often given by the Greek letter, small sigma) is a constant given as 5.67 x 10^-12 W(atts) × cm^-2 × ¡K^-4. Strictly, this equation holds only for perfect blackbodies.

The quantity of radiant emission, and thus the effective temperature that is sensed, is also controlled by the emissivity of the object in the spectral region of interest. Emissivity is a dimensionless number that expresses the ratio of the radiant flux of a real material F_R to the radiant flux of a perfect blackbody F_B (one that completely absorbs incoming radiant energy, with none being partitioned into transmittant or reflectant components), or F_R/F_B = . It is a measure of the efficiency of emitted radiance of any real body to that of a perfect radiator (for which = 1.000). Values of vary from 0 to 1 and are spectrally dependent, i.e., can change with . Here is an example comparing the spectral radiant emittance of the common mineral quartz to a perfect blackbody when both are at thermal equilibrium at a given temperature (here, at 600 °K).

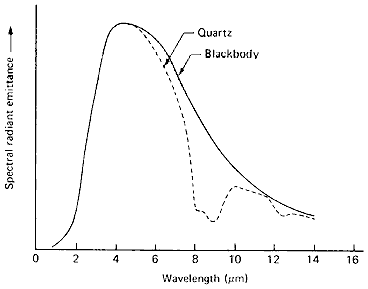
From T.M. Lillesand and R.W. Kieffer, Remote Sensing and Image Interpretation, 2nd Ed., © 1987. Reproduced by permission of J. Wiley & Sons, New York.

The sharp decrease in in the 8-10 µm region noted for quartz and other silicates is a "reststrahlen" effect (decreased emission) related to thermally induced stretching vibrations associated with silicon-oxygen bonds. In general, for opaque materials, , where rho is the materials optical reflectance. Thus, as , with high reflectance of radiation (poor absorptance), the emittance will be low (thus, thermal radiation decreases). Water, which has a high emissivity in the thermal infrared in the 8-10 µm interval, is a poor reflector over that range; quartz (and many silicate rocks) is a good emitter at lower thermal wavelengths but poor in this interval. From this, one might predict that rock surfaces would appear darker than water in the 8 -10 µm interval but this holds only for certain conditions, as we will shortly see.

The radiant (sensed) temperature differs from a body's kinetic (internal) temperature according to the relation ; for real bodies (known as gray bodies) radiant temperatures are always less than kinetic temperatures. Thus, checking the figure below, the radiant temperature is significantly higher for a blackened surface (high ) than for a shiny surface (lower ), even if the two materials are at the same kinetic temperature.

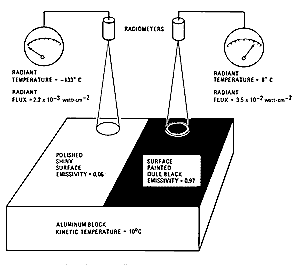
From F.F. Sabins, Jr., Remote Sensing: Principles and Interpretation. 2nd Ed., © 1987. Reproduced by permission of W.H. Freeman & Co., New York City.

---

[an error occurred while processing this directive] [an error occurred while processing this directive]