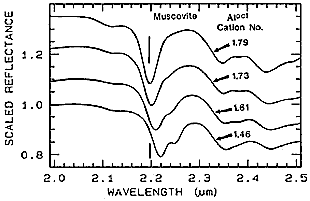
So far, the spectral plots displayed on the preceding page are mostly those of pure phases irradiated under laboratory conditions. Even so, for the same species there can be notable physical and/or chemical variations, e.g., ones related to color or from foreign coatings (such as iron rust), so that a single spectrum, while containing the dominant and diagnostic absorption features for a species, is a standard that must be generalized. Straightforward chemical changes (many minerals, for example, allow for substitutions of one element or ion state at lattice sites by other elements, so that the formula for such materials is itself variable) can significantly modify the spectrum. Take, for instance, the progressive substitution of Aluminum in certain octahedral sites that occurs in the common mica, Muscovite. Note how this affects the principal absorption trough at 2.2 µm. Again, the curves are offset.

The size range of individual mineral grains or crystals can have a major effect on the characteristic spectral curve of the same species. This usually influences the total reflectance but can also modify the depth of an individual absorption feature. Consider the effect of grain size (in µm) for finely ground samples of the same specimen of a pyroxene species (there is no offset applied to these curves).

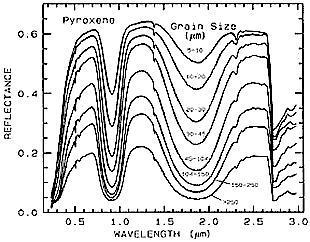
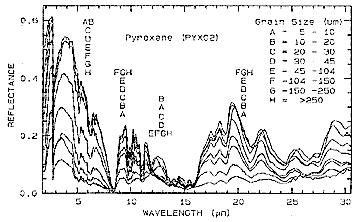
As the grain size enlarges, the reflectance diminishes, although the absorption troughs remain relatively constant . Two factors control this effect: the larger grains allow more absorption and the smaller grains provide a higher proportion of surface area available as reflectors. Rather unexpectantly, there is a broad reversal in the relative reflectance as a function of grain size when the same material is examined in the mid-IR, as shown here:

As we saw earlier in this Section, mixed pixels are the rule for most space images and become ever more troublesome as resolution increases. This problem can be even greater when a single spectral curve is acquired for the features and classes normally present in a pixel representing Landsat MSS or TM resolutions. The resulting spectral plot will show a variety of absorption troughs, some of which can be matched to individual phases (classes) whereas others may lie in nearly the same wavelength positions, but are simply certain bands present in common to the several phases. The reflectance at any given wavelength is likewise a composite average of the proportionalized phases contributing to the mixture.

To illustrate this for two simple cases, observe these curves. The first is just a series of a two phase mix in which the clay mineral Montmorillonite is progressively diluted with charcoal which has a spectral curve with no absorption troughs and an overall low reflectance.

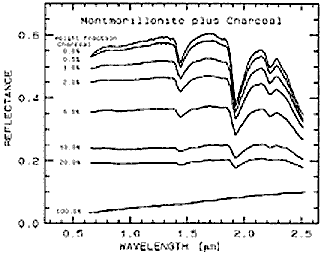
The reflectances are absolute (no offsets). The result of adding the black charcoal to the whitish Montmorillonite is to reduce the depths of the absorption troughs. Above 20% charcoal, the toughs all but disappear owing to the dominance of charcoal in reducing reflectance.

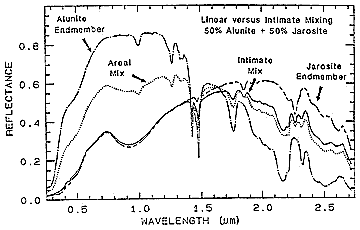
Now look what happens when two very similar minerals, Alunite (a potassium sulphate also containing aluminum) and Jarosite (same, except iron replaces the aluminum) are mixed in two different ways: Areal - computed as a linear equal combination of the two end members; Intimate - actually combined and thoroughly intermixed and then irradiated under laboratory conditions. The darker (yellow-brown) Jarosite has a lower reflectance continuum at the shorter wavelengths but becomes higher at longer wavelengths. In a 50-50 mix, this darker phase predominates, so that the reflectances are (like the effect of charcoal) controlled almost entirely by Jarosite.

From the above considerations, it is obvious that practical remote sensing dependent upon imaging spectrometers and hyperspectral data acquisition is especially sensitive to many variables including foremost the mixed pixel problem. Because the spectral curves that can be derived from sensors such as AVIRIS will vary "all over the place" from pixel to pixel as the combinations of surface features change over the scene, some method(s) of reducing the data to meaningful components that can be assigned to their proper classes are needed. Complex spectral containing contributions from a variety of phases (in a single 30 meter square pixel soil, water, vegetation, buildings, etc. can mutually occur) must be simplified so that the identity and proportions of each can be extracted. Fortunately, with effective mathematical models and computer processing, this task can be done with surprising effectiveness.

This subject of hyperspectral data reduction and analysis is specialized and somewhat complicated, so that only an outline of the approaches used will be offered here.

The starting point - and the key - is to develop a Spectral Library. This consists of literally thousands of individual spectral curves obtained by spectrometers applied to discrete (as much as possible, "pure") materials and classes in laboratory and field settings. This has built up over the years as a data collection developed from many observations by numerous groups. Best known in the U.S. is the library assembled by the Spectroscopy Lab of the U.S Geological Survey in Denver. (For more information, check their Home Page).

From such information, spectral feature identification algorithms have been devised to quantitatively analyze hyperspectral data acquired during aircraft overflights. The U.S.G.S. has put together such a program known as Tetracorder which contains various routines that systematically reduce the raw data to specific identifications. It convolves individual fits of library curves to the hyperspectral data obtained from a mission. In some instances, a complex (composite) curve can be analyzed by appropriate algorithms that break it into a set of "end member" curves, each representing a material or class that is a component of the curve. Band locations (indexed to the wavelength at the bottom of the trough) and depths are calculated, using a continuum base as reference. The weighted fit leads to correlation coefficients that are numerically fixed by a least squares routine. Band ratios can also prove helpful.

Since spectral band widths may be broad, analysis of many individual channels (for AVIRIS, 224 spread continuously from 0.38 to 2.5 µm) is customary. However, not all such channels need be sampled for certain problems. If the task is to identify a group of minerals in an alteration zone in a mining district located in a vegetation-sparse region, the critical interval between 2.1 and 2.5 µm containing enough diagnostic absorption bands may suffice to identify them. For some identifications, data from 2, 3, or a few more channels may be sufficient to identify a particular class in compositional detail. Examine this plot that shows variations in a band bottom point wavelength as a function of compositional variations in pyroxene minerals present in an area undergoing mineral analysis.

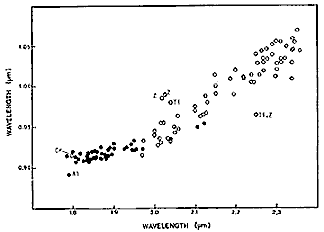
From such data, correlation coefficients relating composition to wavelength are devised using least squares statistics.

Of course, it is usually not expedient to plot spectral curves for every pixel in a mission data set. Instead, the spectral data serve to pinpoint the individual materials present in the pixel and then to display the results in a map or image - the usual display type in presenting the results of scene analysis. If the spectral resolution is high (a few meters), then there is commonly a dominant class assigned to each pixel. In the real world to be pictured, that dominance may extend over many pixels, leading to a hyperspectral image that has much the same characteristics as we see in typical Landsat scene. But, the ability to "fine-tune" the class identities, and to record separately something of the nature of the mix, are the great advantages that have derived from the emergence of imaging spectroscopy as a significant improvement in sensor technology for remote sensing.

---

[an error occurred while processing this directive] [an error occurred while processing this directive]