(Before beginning this long page, a review of page I-8 in the Introduction could be helpful.)
Black and white photographs start with exposure of a light-sensitive film to incoming electromagnetic radiation (light) - selected from some part of the spectral range from ultraviolet through visible into the near infrared. The optical system of the camera focuses the light reflected from the target onto the focal plane (plane of focus). The film is held flat at the plane of focus and the light activates positions in the film area in the same geospatial relation as the radiation photons had in leaving their starting points from their surfaces within the scene. The exposure recorded is a function of many variables. The three principal sets of variables are associated with the scene, the camera, and the film.:
(aperture, dependent on diaphragm width) admitting light; the duration of light admission (controlled by an open/shut shutter); the optical characteristics of the lens: the varying distance from lens to film (focal length f) at which focus is sharpest; the adjustment of this light-gathering system for film response (ISO, formally ASA values);
One general equation for exposure is:
Black and white film consists of a base or backing coated by an emulsion composed of gelatin in which are embedded tiny crystals of silver halides (commonly, Silver Chloride, AgCl) together with wavelength sensitive dyes. The dyes respond to segments of the EM spectrum (UV; visible; visible/near IR; special films can respond to photons from shorter or longer wavelengths, as for example, X-ray film). When a number of photons strike a halide crystal, electrons are knocked loose from some of the silver (Ag) atoms present, ionizing them; the number thus activated depend on the brightness (intensity) of the radiation. The part of the spectral range selected can be controlled by using color filters over the lens. These admit radiation over limited segments of the spectrum. This is a photochemical reaction which conditions the halide grains for later chemical change, forming an intermediate "latent image" (invisible but ready to appear on development). Developing begins by immersing the film in an alkaline solution of specific organic chemicals that neutralize the electrons and reduce Ag+ ions into minute grains of black silver metal. The number of such metallic grains in a given volume determines the film (negative) density; for parts of the emulsion receiving more light, the density (darkness) of the film will be greater. In the developing process, the ion conversion must be stopped at some point using an acidic stop bath. Any silver halides remaining undeveloped are next removed by chemical fixing; volumes in the thin film that saw little exposure (fewer photons) will end up with minimal silver grains and thus appear as light and clear in the film negative. The development process - and hence relative densities in the negative - can be controlled and modified by changes of such variables as solution strengths, developer temperatures, and times in each processing step.
The negative must next be used to make a separate positive black and white print - in which dark tones correspond to darker areas in the scene, and light to light. This is done during the printing process. A print (or a positive transparency) consists of an emulsion backed (in a print) by paper. White light is transmitted through the negative onto the print material. Clear areas will allow much light to pass and strike the print which on development will produce high densities of dark (silver-rich) tones; thus the initial low levels of photons coming from the target (relative darkness) will ultimately produce a print image consisting of many silver grains that make the areas affected dark. Bright target areas in turn, being represented by dark areas in the negative that prevent light from passing, will be expressed as light (whitish to light gray) tones in the print (little silver, so that the whiteness of the paper persists). Once again, the relative levels of gray or increasing darkness can be controlled in the development process by changing the same variables as above, by modifying exposure times, by using print papers with specific radiation responses and by using filters with different spectral response (minimizing passage of certain wavelengths) or light transmission. Thus, different average tonal levels of the print can be chosen, and, more important, the relative levels of gray (tones) can be adjusted to present a pictorial expression called contrast (which determines whether a scene with variable colors and brightness appears "flat" or is presented with wide ranges of light-dark that aid in discriminating different features). Contrast is determined as the ratio of density to (logarithmic value of) exposure; this can be plotted in the Hurter-Driffield [H-D] curve which is a straight line with some slope angle g for a range of exposures but becomes curved at high and low exposures.
Black and white films can be exposed under a condition that converts them into multispectral images. This is done by using color filters that pass limited ranges of wavelengths (bandpass filters) during exposure. As was explained back in the Introduction to this Web Site, a red filter, for example, will pass mainly radiation in the red and nearby regions of the visible spectrum. Reddish objects produce high exposures that appear in dark tones on a negative and will reappear as light tones in black & white prints or in red on color positive film (why this is so different from the response of black and white film, is described in the following paragraphs); green will appear as dark in a black & white multispectral image representing the red region and as dark or subdued green in a color multispectral version. Multispectral positive transparencies for different color bands can be projected using several color filters onto color print paper to produce natural or false color composites, as described previously in the Introduction.
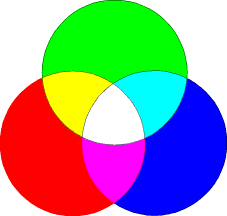
How color film is used to produce color images involves some different concepts, although many of the same factors and mechanisms are still valid. Starting with the three additive primary colors - red, green, and blue - or the subtractive primary colors yellow, cyan and magenta, other colors can be made by using the principles of either the color addition or the color subtraction process. Look at these diagrams:
 |
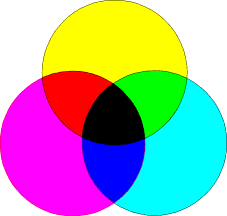 |
| Additive Color Model | Subtractive Color Model |
Color addition works when the primary colors are superimposed on one another. For example, if you shine a green light and a red light on the same spot on a white wall, you will see some shade of orange or yellow, depending on the relative intensity of the red and green illumination. If you add a third blue light to the spot, you will see white or some shade of gray. Your computer display works this way. To create a color, you can typically choose a number between 0 and 255 to indicate how much of each of the three primary colors you want. If your display board has sufficient memory, you will have 2553 colors to choose from.
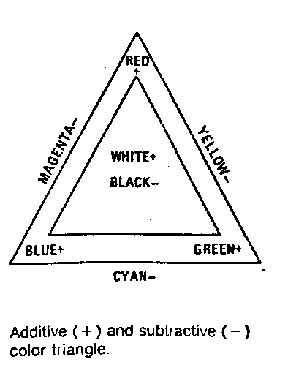
In subtractive color, filters are used to remove colors. A yellow filter removes colors other than yellow, similarly for cyan and magenta filters. If one superimposes all three filters, no or little visible light gets through so either black or dark gray is the result. By combining pairs of the subtractive primary colors, each of the additive primary colors can be created. Magenta and Yellow produce Red. What corresponds to Cyan and Magenta and Yellow and Cyan?
The principles of color subtraction apply to color-sensitized film. This film consists of emulsion layers containing silver chloride treated with light sensitive dyes, each responding to a limited wavelength range; these layers on development act as subtractive filters. Thus each layer of the film responds to different sections of the scene's spectrum. These layers are stacked, respectively, as follows: blue-sensitive layer, yellow filter layer (to screen out UV and blue from passing into the next layers; omitted from the diagrams below), then green- and red-sensitive layers.
From F.F. Sabins, Jr., Remote Sensing: Principles and Interpretation. 2nd Ed., © 1987. Reproduced by permission of W.H. Freeman & Co., New York City.
Referring to the above diagram, when a shade of red passes through a color layer sensitized to cyan (a blue-green, the complementary color to red; the sum of any primary and its opposing complement always equals white), its absorption will activate the dye/silver grains in that layer to produce in a negative cyan tones in areas associated spatially with reddish objects in the scene. In color film, the three subtractive color layers are stacked together (a fourth serves a special purpose described below) on top a clear base. To guide you in reasoning through production of other colors, check this schematic diagram:
From F.F. Sabins, Jr., Remote Sensing: Principles and Interpretation. 2nd Ed., © 1987. Reproduced by permission of W.H. Freeman & Co., New York City.
Thus, in like manner, light from a blue subject reacts with the yellow layer to produce a yellow shade (this complementary color is made of red and green) for its area on the negative. To test your understanding, from the diagram, you set up the response for green objects (magenta, a bluish-red, is a mix of red and blue). No doubt you can see an obvious rule working here:
From F.F. Sabins, Jr., Remote Sensing: Principles and Interpretation. 2nd Ed., © 1987. Reproduced by permission of W.H. Freeman & Co., New York City.
As evident in the diagram, each primary color activates the layer containing the subtractive color opposite it . Several other rules or observations:
To comprehend how a color print is made, follow this set of arguments: During passage of white light through the color negative to initiate the printing, cyan areas transmit that light through the cyan layer of the print film (called the positive or reversal film) but not through the magenta or yellow areas, exposing each so that it assumes its color. Since the sum of yellow + magenta is red, on development the print film will be red in the areas that are cyan in the negative. The same line of reasoning applies to the magenta and yellow areas on the negative, with green and blue resulting. If the negative has both yellow and magenta occupying the same areas on the two superposed layers, the results will be green + green = yellow, and so forth for other non-primary colors. To reinterate, the blue from the cyan of the negative activates first the yellow layer (sensitive to blue which is absorbed) and then the magenta layer (sensitive to green) but the cyan bottom layer is not sensitized by the cyan light itself (passes through), becoming clear on development; this statement can be tailored for each of the other two negative colors.
Color transparencies are generated by a similar color reversal technique but without the need for a negative. First, the exposed transparency film is developed to cause it to initially act as a negative image (conversion of the sensitized silver chloride/dyes to color grains) in each of the three color emulsion layers. Film is then re-exposed to white light to render any remaining silver halide developable. This latent positive image is then chemically coupled or combined with color dyes to produce a positive color image in each layer. The film is next treated in a bleach which, without affecting the dyes, converts silver into soluble salts and removes unused dye couplers, while removing the initial yellow filter layer. A red subject forms a magenta and a yellow image pattern on the green- and blue-sensitive layers. When white light projects through this transparency, yellow and magenta layers absorb blue and green respectively, allowing red to appear in the projected image where red should be spatially. (Likewise for the other colors.)
Other systems of color production have been devised. One mentioned briefly here is the IHS system, in which:
Let's move now from the spectral to the spatial. Scale, mentioned before, is just the comparison of the dimensions of an object or feature in a photo or map to its actual dimensions in the target. Scale is stated in several ways, such as "6 inches to the mile", "1/20000", and, most common "1:2000". This means that one measurement unit in the numerator (image or map) is equivalent to the stated number of that unit in the denominator (scene). Thus, 1:2000 simply states that 1 of anything, such as an inch, in the photo corresponds to 2000 inches on the ground or air (cloud). Or, 1 cm is equivalent to 20000 cm. "6 inches to the mile" translates to "6 inches in the photo represents 63360 [5280 ft x 12 in/ft] inches in the real world", but can be further reduced to 1:10560 (both 6 and 63360 are divisible by 6). Note that if a photo of a given scale is enlarged or contracted, say by projection as a transparency onto the screen, then one inch on the screen no longer corresponds to the same denominator number but now represents some other number determined by the magnification factor; however, the effective resolution, the area covered, and relative details remain the same.
The scale of the aerial photo, expressed as its Representative Fraction (RF), is determined by the height of the moving platform and by the focal length of the camera, according to this equation: RF = f/H*, where H* = H - h, with H = height (elevation with reference to sealevel) of the camera and h is the height of a reference point on the surface, so that H - h is the distance between platform and point (assuming a flat ground surface; in rugged terrain, scale in effect varies with the different elevations). It can also be shown that RF is also proportional to resolution and distance ratios as given by RF = rg/rs = d/D, where rg is ground resolution (in line pairs per meter; see below) and rs is the sensor system resolution (in line pairs per millimeter); d is the distance between two points in the photo and D is the actual distance between these points on the ground (the definition of scale).
The roles of f and H* can be further elucidated with the aid of the next diagram which, although not strictly correct in terms of optics and simplified to two dimensions, does allow visualization of the effects of changing focal length and platform height:
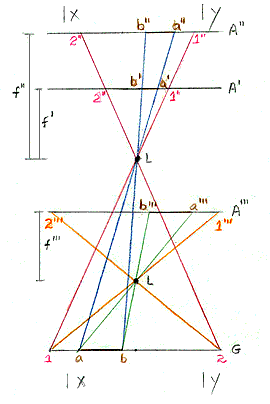
Lines such as 1-1" or a-a' are light rays passing through the lens L; G is the ground; A' is at the focal plane (holding the film) for a focal length of f' and A" is the shift of this plane to a new value of f "; A"' is the location of the focal plane for a case in which the lens L is now at a lower elevation. A line on the ground, a-b, passing through lens L is focused on plane A' such that it has a film dimension of b'-a' (note that it is reversed in position but this does not matter since a transparent negative can be turned over). When the focal length is lengthened to f" to bring the focus onto A", b'-a' expands to b" - a";. Look next at what happens when the camera (and airplane) is lowered to the A"' position: a-b in this new arrangement (where L, the lens location relative to the film is the same distance as case 1, so that the focus, or focal length, is once more f ', i.e., f"' = f') now is expressed by b'''-a''', which for these conditions is even longer than b"-a". In these situations the frame size of the film (x-y in the two dimensional simplification) remains the same. Therefore, when x-y is at the A" location, the fraction of the scene imaged is reduced by loss of the outer parts and b"-a" occupies a larger segment of it. In the A"' case, the size of film needed to display all of 1-2 would be even greater, so that x-y now would enclose even less of the scene. The A"' image, held to the x-y limit, would be larger scale than an A' image and the A" image is also (less) larger. Keep in mind that the dimensions shown on the line G are ground-sized whereas those in A', A", and A"' are film-sized, reduced relative to ground distances by the scales of the photographs.
These relations can be summarized in a mnemonic: Long is large/Low is large; Large is small. This is interpreted as follows: The scale is larger (denominator becomes smaller) as the focal length is made longer or as the platform is lowered; a large(r) scale image will cover a small(er) ground area (with increased resolution). To appreciate how scale affects scene content, you may wish to return to the various photos that were brought on-line in the previous page; the scale of each is printed alongside it.
Resolution has a popular meaning but is best defined in a technical sense. We normally think of resolution as the ability to separate and distinguish adjacent objects or items in a scene, be it in a photo or just what we view. The resolution is specified in terms of the smallest such features we can discriminate. But, resolution is influenced by the contrast between items; if they are the same color, they might be hard to separate; if sharply different in color, tone, or brightness, they are more easily picked out. Shape also is a factor. A rigorous definition of resolution relies on the ability to separate adjacent alternating black and white thin lines in a target. The resolution of a film is determined in a laboratory setting by photographing placard sized charts containing black lines with different spacings on a white background (or the reverse); the smallest spacing in which pairs can be discriminated determines the resolution.
Such a target can actually be placed in the scene (for example, painting black lines with different spacing on a concrete airport runway or road) to determine resolution under aerial conditions. Ground resolution is then given as the number of black/white line pairs within some width (normally one meter) that can just be discerned in aerial photos taken at a particular height. Depending on camera, film resolving power, and platform height (the system), in the photo the pair will either blend visually (not resolvable) or can be distinguished. System resolution rs (in which the effects of sensor and film factors are combined) is expressed in line pairs/mm within the print. A formula for ground resolution rg (in line pairs/meter) applicable to just separable ground lines is:rg = f x rs/H where rs. A typical example is a case where the lens focal length has a value of 150 mm, system resolution is 60 line pairs/mm, and height is 3000 meters, so that Rg would be 3 line pairs/meter; from the relation 1 line pair/rg = width on ground of 1 line pair, this width here would be 0.33 m (each line would be half that) . This means an object on the ground that has a dimension of 0.165 m (about 6.5 inches) could, if it contrasts with its surroundings, be barely picked out by a camera whose lens has a focal length of 150 mm when the aircraft is flying at an altitude of about 10000 ft, using a film of appropriate resolving power. If the aircraft were flying higher, this sized object could not be detected.
Resolution in film (both negatives and prints) is governed, in part, by the size distribution of the silver grains. In Landsat MSS/TM, and other electronic sensors, image resolution is closely tied to the size of the pixels as scanned or to the dimensions of individual detectors in the arrays of Charge-Coupled Detectors (CCDs), as on SPOT. At first thought, it would seem that objects smaller than the ground dimensions represented in an individual pixel/detector cannot be resolved; however if the spectral characteristics of a subresolution spot on the ground are sufficiently different from surrounding areas, they can effect the average brightness of the pixel so that it is visible in the image. An example of this are roads that are narrower than a 30 meter (98 ft) TM pixel, yet are quite visible in a TM image.
In an aerial photo, features at ground points off the principal point (optical center, usually at nadir if the photo was taken when the viewing axis was perfectly vertical or normal to a flat surface) that are viewed along slant directions may appear to be leaning away from the center, especially if they are tall (like buildings) or have high relief. This distortion is emphasized even more if the aircraft is flying low to acquire large scale photos. This is one type of displacement, and is evident near the edges in the 1:4000 aerial photo of a neighborhood in Harrisburg shown on p. 10-1. Other modes of displacement, such as apparent lateral movements of image points along slopes of differing angles, are considered in Section 11, which explores 3-D aspects relevant to stereo viewing and photogrammetric mapping.
Aerial photo missions can be flown at any time during the day but usually take place between about 10:00 AM and 2:00 PM (in summer to avoid afternoon storms) and commonly in the summer because of better weather. Typically, the region to be photographed is traversed along back-and-forth flight lines with pictures acquired at intervals that allow about 50% overlap between successive ones and 20 to 50% sidelap between lines. Film in the camera (which is normally mounted below the plane [usually near its nose]) is advanced automatically at time intervals that are synchronized with the speed of the aircraft. Especially in color photos, but also in black and white, the film image may be degraded by blue and ultraviolet light that is scattered by the atmosphere. This can be reduced by using a haze filter that absorbs the ultraviolet and the very shortest visible blue wavelengths.
NASA has a "stable" of support aircraft that operate various sensors, including cameras, to gather ground reference data for remote sensing experiments (see Section 13 which discusses this). An example of a small-scale image (about 1:150000) obtained during a U-2 flight, which operated at an altitude of about 18000 m (59000 ft) over Utah (resolution about 5 meters), closes this section on aerial photography.
 |
For those of you interested in viewing more aerial-type photos, including perhaps one of your home region, consult the on-line Net Home Page called "Terraserver", sponsored by Microsoft. Aerial imagery, either individual photos or sections of orthophotoquads, of selected large parts of the United States, has been digitized from data collected by the U.S. Geological Survey; resolution ranges from less than 2 to about 12 meters. Imagery for regions in the rest of the world, mainly in Europe, is represented by photos taken with the KVR-1000 camera (resolution: 2 meters) flown on several Russian satellites; these data are now being marketed worldwide as part of their SPIN-2 program. All photos are black and white.
Code 935, Goddard Space Flight Center, NASA
Written by: Nicholas M. Short, Sr. email: nmshort@epix.net
and
Jon Robinson email: Jon.W.Robinson.1@gsfc.nasa.gov
Webmaster: Bill Dickinson Jr. email: rstwebmaster@gsti.com
Web Production: Christiane Robinson, Terri Ho and Nannette Fekete
Updated: 1999.03.15.