The Remote Sensing Tutorial

[an error occurred while processing this directive]

The ElectroMagnetic Spectrum

Most texts on remote sensing begin by giving the reader a survey of the main principles needed to build a theoretical background (mainly in the physics of radiation). While it is important to have such a framework if one wishes to pursue many aspects of remote sensing, we will not delve into this profound subject in much detail at this point (the user interested in more depth of understanding is referred to the three chapters from The Landsat Tutorial Workbook ). Instead, we will offer here only an outline survey of the basics of relevant electromagnetic concepts.

The fundamental unit involved in electromagnetic phenomena is the photon (one form of quanta, as considered in quantum physics). This is the subatomic particle which comprises radiation given off by matter when it is excited thermally, or by nuclear processes (fusion, fission), or by other radiation. Photons, which are without mass, in transfer move at the speed of light: 300,000 km/sec (186,000 miles/sec). As such, these particles also move as waves - hence, they have a "dual" nature. These waves follow a pattern described in terms of a sine (trigonometric) function, as shown in two dimensions in the figure below.

The distance between equivalent points on a wave train is its wavelength. The total number of equivalent points that pass by a reference in a second is expressed by the frequency of that wave (associated terms include cycles per second; hertz). A given photon has a certain amount of energy. This packet of energy (in ergs) is determined by the general Planck equation:

where his the Planck constant (6.6260... x 10^-34 Joules-sec) *and vis a Greek letter representing frequency. Photons travelling at higher frequencies are therefore more energetic. If a material under excitation experiences a change in energy level from a higher level E₂ to a lower state E₁, the above formula would be restated as:

where v has some discrete value determined by (v₂ - v₁); in other words, a particular energy change is characterized by production of emitted radiation (photons) that has some specific frequency v and a corresponding wavelength .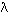

Wavelength is the inverse of frequency (higher frequencies associate with shorter wavelengths; lower with longer), as given by the relationship:

where cis the constant that expresses the speed of light, so that the Planck equation can also be written as

_{* The number 10^-34 (incredibly small) or 10¹² trillion (very large) is a shorthand notation that allows one
to express very large and very small numbers without writing out
all of the digits. It allows one to "normalize" a number by expressing
it in two parts: the first part expresses the value of the number
as a real value between .9999... and 10 exclusive; the second
part of the number tells the number of places to shift the decimal
point to the right or the left. One multiplies the first part
of the number by the power of ten in the second part of the number
to get its value. Consider the second part of the number, values
assigned to the number 10ⁿ where n can be any positive or negative integer. A +n indicates
the number of zeros that follow the number 10, thus for n = 3,
the value of 10³ is 1 followed by three zeros, or 1000 (this is the same as the
cube of 10); 10⁶ is 1000000, i.e., a 1 followed by six zeros to its right (Note:
10⁰ = 1). Thus, 10⁶⁰ represents 1,000,000,000,000,000... out to 60 such zeros. Likewise,
10^-3 (where n = -3) is equal to 0.001, equivalent to the fraction
1/1000, in which there are two zeros (three places) before the
decimal point at 1. ; 10^-6 is evaluated as 0.000001. Any number can be represented as the
product of its decimal expression (between .99999... and 10) and
the appropriate power of 10, (10ⁿ). Thus, 8345 is restated as 8.345 x 10³; the number 0.00469 is given as 4.69 x 10^-3.}

[an error occurred while processing this directive]

Code 935, Goddard Space Flight Center, NASA
Written by: Nicholas M. Short, Sr. email: nmshort@epix.net
and
Jon Robinson email: Jon.W.Robinson.1@gsfc.nasa.gov
Webmaster: Bill Dickinson Jr. email: rstwebmaster@gsti.com
Web Production: Christiane Robinson, Terri Ho and Nannette Fekete
Updated: 1999.03.15.